这一章的内容比较简单，主要介绍了三个东西：PPR, NN和Bayesian-NN。其主要思想在于从输入构造出线性特征，然后对这些特征做非线性组合，用于预测。

Projection Pursuit Regression

PPR是可加模型(additive model)的成员，在线性模型上加一个非线性变换\(g\)，然后把多个这样的模型加起来，形式如下：

\[f(\boldsymbol{x}) = \sum_{m=1}^M g_m (\boldsymbol{\omega}_m^T \boldsymbol{x})\]

如果\(M\)取得足够大，并且选择合适的\(g_m\)，那么PPR可以近似任何连续函数。PPR是一个很general的模型，可以看到如果\(M=1\)，那么类似LR这样的模型就是它的一个特例。

书上用squared loss举例，讲解了PPR的求解方法(Gauss-Newton)：在\(\boldsymbol{\omega}_{old}\)处做一阶泰勒展开后求解minimum，如此迭代直至收敛。

Neural Networks

这一节主要介绍仅有一个hidden-layer的神经网络。假设我们已经把截距加入了各weight中，那么这类NN可以分解为：

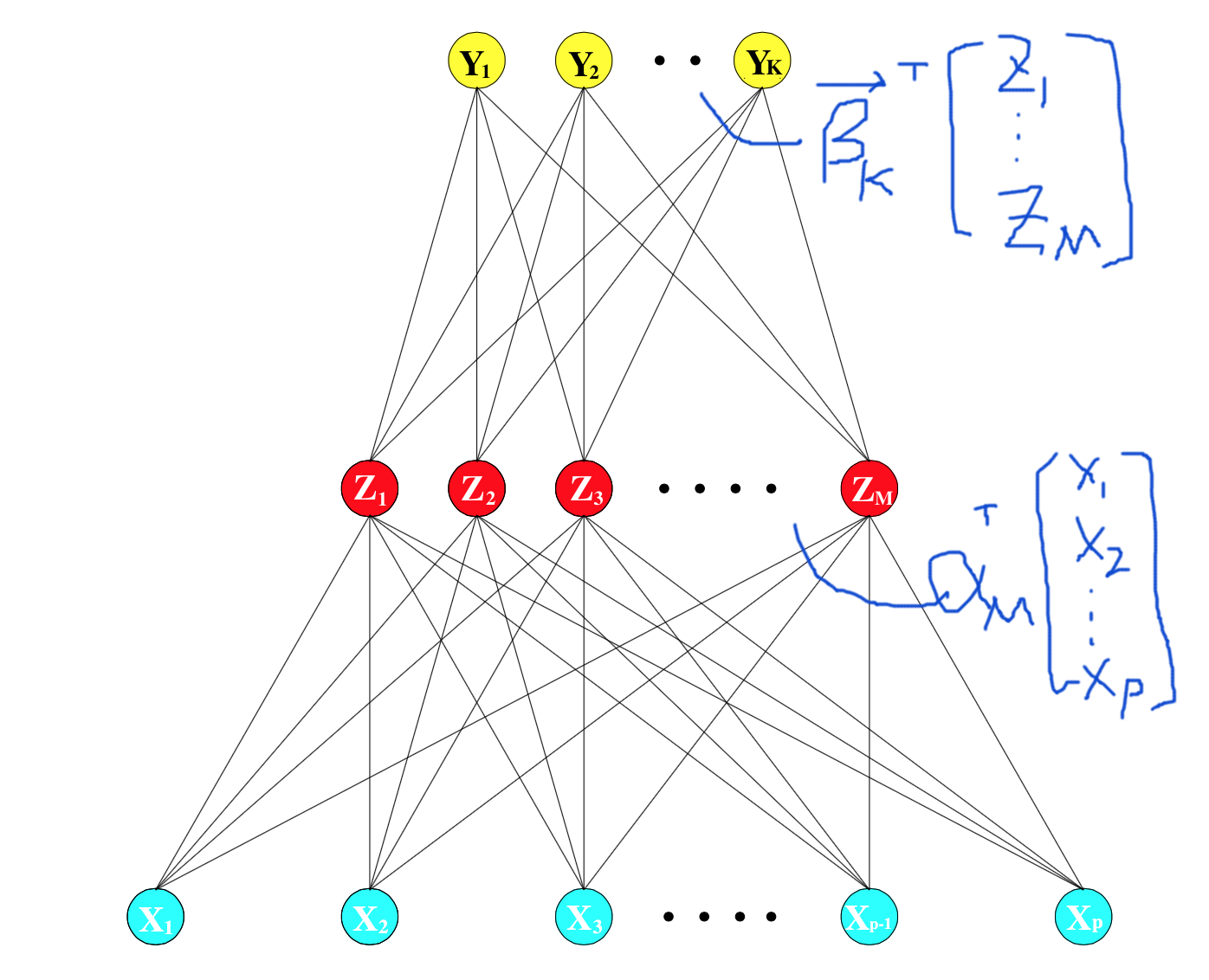
  • Input: \(P\)维向量\(\boldsymbol{x}\)；每一维表现在图上是一个input cell \(x_p\)
  • Hidden(bottom): \(z_m = \sigma(\boldsymbol{\alpha}_m^T \boldsymbol{x}), m=1,2,\dots,M\)；参数为\(\boldsymbol{\alpha}_m\)，\(z_m\)是一个标量，表现在图上就是一个neural cell
  • Hidden(top): \(t_k = \boldsymbol{\beta}_k^T \boldsymbol{z}, k=1,2,\dots,K\)；参数为\(\boldsymbol{\beta}_k\)，\(\boldsymbol{z}\)是由所有\(z_m\)串起来的一个向量
  • Output: \(o_k = g_k(\boldsymbol{t}), k=1,2,\dots,K\)；\(o_k\)是一个标量，表现在图上就是一个output cell，\(\boldsymbol{t}\)是由所有\(t_k\)串起来的一个向量，\(g_k\)例如softmax函数\(g_k(\boldsymbol{t})=e^{t_k} / \sum_{l=1}^K e^{t_l}\)

注意到这里hidden-layer和PPR的模型形式是一致的，区别在于PPR的函数\(g\)是非參的，而这里的\(\sigma(\cdot)\)则是一个更简单的函数；另外当\(\sigma(\cdot)\)是一个identity函数的时候，NN就退化为一个线性模型了。

NN的back-propagation算法是求导链式法则的自然推导结果，以单个input sample \(P\)维向量\(\boldsymbol{x}\)，\(K\)维output向量\(\boldsymbol{o}\)为例，采用squared-loss，对第\(k\)个output，有：

\[\begin{equation*} \begin{split} R_k &= \| y_k - o_k \|_2^2 = \| y_k - g_k(\boldsymbol{t}) \|_2^2 \\ \frac{\partial R_k}{\partial t_k} &= -2(y_k-g_k(\boldsymbol{t}))g_k^{\prime}(\boldsymbol{t}) \\ &\triangleq \delta_k \\ \frac{\partial R_k}{\partial \boldsymbol{\beta}_k} &= \frac{\partial R_k}{\partial t_k} \cdot \frac{\partial t_k}{\partial \boldsymbol{\beta}_k} \\ &= \delta_k \cdot \boldsymbol{z} \\ \frac{\partial R_k}{\partial \boldsymbol{\alpha}_m} &= \frac{\partial R_k}{\partial t_k} \cdot \frac{\partial t_k}{\partial \boldsymbol{\alpha}_m} \\ &= \frac{\partial R_k}{\partial t_k} \cdot \frac{\partial t_k}{\partial z_m} \cdot \frac{\partial z_m}{\partial \boldsymbol{\alpha}_m} \\ &= \delta_k \cdot \beta_{km} \cdot \sigma^{\prime}(\boldsymbol{\alpha}_m^T \boldsymbol{x}) \cdot \boldsymbol{x} \\ &\triangleq s_m \cdot \boldsymbol{x} \end{split} \end{equation*}\]

其中\(\beta_{km}\)表示\(\boldsymbol{\beta}_k\)的第\(m\)个分量。

可见，上一层的\(\delta_k\)在下一层计算的时候可以继续被用到，同样的，如果这个NN不止一层hidden-layer，那么\(s_m\)在下一层也可以被复用。back-propagation的好处在于能直接在NN结构上进行优化，直观，容易写程序，各层参数的导数计算可复用，减小了计算量。

需要注意的是，当我们更新\(\boldsymbol{\alpha}_k\)的时候，使用的\(\beta_{km}\)应该是更新前的值。始终记住，bp本质上是对loss直接求导的高效实现，对loss求导的时候岂有先更新一部分参数，然后把这部分参数代回再求导的道理？

conjugate gradients和variable metric methods可以获得更快的收敛速度，并且不需要求二阶导。

最后介绍了一些NN的问题：

  • 初始值通常选取0附近的随机值。0求导后还是0，而选得太大通常会产生比较差的结果
  • 解决overfitting：使用early-stop和regularization
  • 单个输入样本的各维度做标准化，使其均值为0，标准差为1
  • 由于NN是非凸的，容易陷入局部最优点。解决方法包括avg-predictions, avg-weights, (perturbed) bagging. 优劣3>2>1

Bayesian Neural Networks

最后一节虽然标题是Bayesian NN，但并没有介绍具体的细节。但我觉的有两个地方值得简单说明一下：

在已知posterior的情况下sample得到predictive distribution

\[P(Y_{new} \vert X_{new}, \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr}) = \int P(Y_{new} \vert X_{new}, \theta) P(\theta\vert \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr}) d\theta\]

如果后验\(P(\theta\vert \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr})\)是已知的话，那么直接用Monte Carlo方法就可以得到（不需要构造马尔可夫链）。不管是MC还是MCMC（稳定后），sample得到的\(\theta^{(1)}, \theta^{(2)},\dots,\theta^{(S)} \sim \mathrm{i.i.d} P(\theta\vert \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr})\)，都有性质

\[\frac{1}{S} \sum_{s=1}^S g(\theta^{(s)}) \to \mathbb{E}[g(\theta)\vert \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr}] = \int g(\theta) P(\theta\vert \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr}) \quad as \quad S -> \infty\]

因此，我们可以用\(\sum_{s=1}^{S} P(Y_{new} \vert X_{new}, \theta^{(s)})\)来近似分布\(P(Y_{new} \vert X_{new}, \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr})\)

或者更一般的，如果我们需要得到这个predictive分布的样本，那么就这样来sample：\(Y_{new}^{(s)} \sim P(Y_{new}\vert X_{new},\theta^{(s)})\)。值得注意的是，此时变量\(Y_{new}^{(s)} \sim P(Y_{new}\vert X_{new}, \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr})\)，是边缘分布，这是因为\(Y_{new}^{(s)}\)的sample每次都依赖不同的\(\theta\)，”condition on different values” 意味着 “margin on that variable”；而两个变量的pair：\((\theta^{(s)},Y_{new}^{(s)}) \sim P(Y_{new},\theta\vert X_{new}, \boldsymbol{X}_{tr}, \boldsymbol{y}_{tr})\)，同样也是边缘分布。

Bayes(MCMC), Boosting, Bagging的关系

这一节作者寥寥几句给出了很深刻很有意思的观点：Bagging和Boosting虽然是非参贝叶斯，但和MCMC有非常类似的效果。MCMC是训练数据保持不变，根据当前的参数估计，对模型参数进行扰动（修正）；Bagging则扰动数据（通过bootstrap i.i.d重抽样），然后用新数据重新修正模型参数；Boosting和Bagging类似，区别在于每轮的新模型和上一轮的模型结果相关，因此其采样数据不是i.i.d的。这三个模型都可以用下面的形式来归纳：

\[\hat{f} = \sum_{l=1}^L w_l \mathbb{E}(Y_{new}\vert \boldsymbol{x}_{new}, \hat{\theta}_l)\]
  • MCMC：\(w_l = 1/L\)，\(\theta_l\)是从posterior分布中sample出来的；
  • Bagging：\(w_l = 1/L\)，\(\theta_l\)来自对bootstrap重抽样数据的学习；
  • Boosting：\(w_l = 1\)，\(\theta_l\)是对模型持续优化得到的。