Laplace Approximation

这一部分是BIC推导的基础，主要参考PRML 4.4节。

在Bayesian框架中，我们常常会遇到后验分布形式较为复杂，导致诸如无法积分之类的问题。有很多近似方法来解决这类问题，比如EM、MCMC等等。这里要介绍的Laplace近似，试图用一个高斯分布来近似任意分布\(p(z)\)，假设

\[p(z) = \frac{1}{Z} f(z)\]

其中\(Z = \int f(z) dz\)是归一化因子，后面会看到，在Laplace近似中，并不需要知道这个归一化因子。

现在我们的目的是要用高斯分布来近似\(p(z)\)，很显然，高斯的波峰应该和\(p(z)\)的波峰契合，于是我们首先求得\(p(z)\)的驻点(mode)\(z_0\)，即\(p^{\prime}(z_0) = 0\)，也即

\[\frac{df(z)}{dz}\bigg |_{z=z_0} = 0\]

我们知道，高斯分布有一个性质：取对数后就是随机变量的二次函数。于是我们就想到对原分布的对数在点\(z_0\)处做泰勒近似：

\[\ln f(z) \simeq \ln f(z_0) - \frac{1}{2} A(z-z_0)^2\]

其中

\[A = -\frac{d^2}{dz^2} \ln f(z) \bigg |_{z=z_0}\]

泰勒展开的一次项由于\(f^{\prime}(z_0) = 0\)，自然就没有了。取指数，我们得到

\[f(z) \simeq f(z_0) \exp \left \{ -\frac{A}{2}(z-z_0)^2 \right \}\]

这样乘上一些常数，我们就能凑出高斯分布的形式：

\[q(z) = \left( \frac{A}{2\pi} \right)^{1/2} \exp\left\{ -\frac{A}{2}(z-z_0)^2 \right\}\]

现在\(q(z)\)就是我们要找的近似高斯分布。有几个地方特别说明一下：

  • 我们在做Laplace近似的过程中并没有使用到归一化项\(Z\);
  • 驻点\(z_0\)通常没有解析解，可以通过数值优化算法求解;
  • 如果\(p(z)\)是一个多峰分布，那么任选一个驻点做Laplace近似，当然在这种情况下会导致较差的近似性能;
  • Laplace近似强烈依赖于原分布的局部性质，缺乏『全局观』，这也是其主要局限.

如果推广到\(M\)维，那么Laplace近似的表达式如下：

\[\begin{equation} \label{eq:laplace-approx} q(\mathbf{z}) = \frac{|A|^{1/2}}{(2\pi)^{M/2}} \exp\left\{-\frac{1}{2}(\mathbf{z}-\mathbf{z}_0)^T A (\mathbf{z}-\mathbf{z}_0) \right\} \end{equation}\]

其中\(A\)是Hessian矩阵：

\[A = - \nabla \nabla \ln f(\mathbf{z}) \big |_{\mathbf{z} = \mathbf{z}_0}\]

有了\(f(\mathbf{z})\)的近似表达，我们可以进一步求得归一化项\(Z\)：

\[\begin{equation} \label{eq:laplace-approx-normalization} Z = \int f(\mathbf{z}) d\mathbf{z} \simeq \int q(\mathbf{z}) d\mathbf{z} = f(\mathbf{z}_0) \frac{(2\pi)^{M/2}}{\vert A \vert^{1/2}} \end{equation}\]

BIC

现在让我们从Bayesian角度来看model selection这个问题。假设我们有一堆待选模型\(\mathcal{M}_m\)，\(m=1,\dots , M\)，以及每个模型有一个对应参数向量\(\boldsymbol{\theta}_m\)，给定训练集\(\mathcal{D}\)，我们希望选择一个具有最大后验概率\(P(\mathcal{M}_m \vert \mathcal{D})\)的模型。利用贝叶斯公式，有：

\[\begin{equation*} \begin{split} P(\mathcal{M}_m \vert \mathcal{D}) &\varpropto P(\mathcal{M}_m) \cdot P(\mathcal{D} \vert \mathcal{M}_m) \\ &\varpropto P(\mathcal{M}_m) \cdot \int P(\mathcal{D} \vert \boldsymbol{\theta}_m, \mathcal{M}_m) P(\boldsymbol{\theta}_m \vert \mathcal{M}_m) d\boldsymbol{\theta}_m \end{split} \end{equation*}\]

若假设\(P(\mathcal{M}_m)\)是常数，那么\(P(\mathcal{M}_m \vert \mathcal{D})\)的大小就仅取决于第二项：

\[P(\mathcal{D} \vert \mathcal{M}_m) = \int P(\mathcal{D} \vert \boldsymbol{\theta}_m, \mathcal{M}_m) P(\boldsymbol{\theta}_m \vert \mathcal{M}_m) d\boldsymbol{\theta}_m\]

现在我们定义：

\[f(\boldsymbol{\theta}_m) \equiv P(\mathcal{D} \vert \boldsymbol{\theta}_m, \mathcal{M}_m) P(\boldsymbol{\theta}_m \vert \mathcal{M}_m)\]

套用(\(\ref{eq:laplace-approx-normalization}\))式，就可以得到：

\[\begin{equation} \label{eq:p-data-given-model} \begin{split} P(\mathcal{D} \vert \mathcal{M}_m) &= \int f(\boldsymbol{\theta}_m) d\boldsymbol{\theta}_m \\ &\simeq f(\boldsymbol{\theta}_m^{(0)}) \frac{(2\pi)^{M/2}}{\vert A \vert^{1/2}} \\ &= P(\mathcal{D} \vert \boldsymbol{\theta}_m^{(MAP)}, \mathcal{M}_m) P(\boldsymbol{\theta}_m^{(MAP)} \vert \mathcal{M}_m) \frac{(2\pi)^{M/2}}{\vert A \vert^{1/2}} \end{split} \end{equation}\]

其中\(\boldsymbol{\theta}_m^{(MAP)}\)是使得\(P(\mathcal{D}, \boldsymbol{\theta}_m \vert \mathcal{M}_m)\)最大的参数，也就是使得后验\(P(\boldsymbol{\theta}_m \vert \mathcal{D}, \mathcal{M}_m)\)最大的参数（差了一个归一化常数）

对(\(\ref{eq:p-data-given-model}\))式两边取对数，并做适当的近似（假设Hessian矩阵\(A\)满秩），可以得到：

\[\begin{equation} \label{eq:bic-prml} \ln P(\mathcal{D} \vert \mathcal{M}_m) \simeq \ln P(\mathcal{D} \vert \boldsymbol{\theta}_m^{(MAP)}, \mathcal{M}_m) - \frac{1}{2} M \ln N \end{equation}\]

\(N\)是训练集的大小。取个负号就得到了BIC的定义式：

\[\begin{equation} \label{eq:bic-esl} \operatorname{BIC} = -2 \cdot \operatorname{loglik} + M \ln N \end{equation}\]

其实不取负也是可以的，PRML上定义的BIC就是(\(\ref{eq:bic-prml})式。只不过(\)\ref{eq:bic-prml})式越大越好，(\(\ref{eq:bic-esl}\))式越小越好。

容易看到，相比AIC而言，BIC对于模型的复杂度惩罚更大（多乘了一个参数个数\(M\)）

VC维

In-sample指标有一个麻烦，就是如何确定参数个数\(d\)的问题，而模型中的参数个数和模型复杂度往往又不是一回事，比如\(I(\alpha_0 + \alpha_1 x)\)有两个可变参数，而\(I(\sin\alpha \cdot x)\)只有一个参数，但显然后者比前者更复杂。

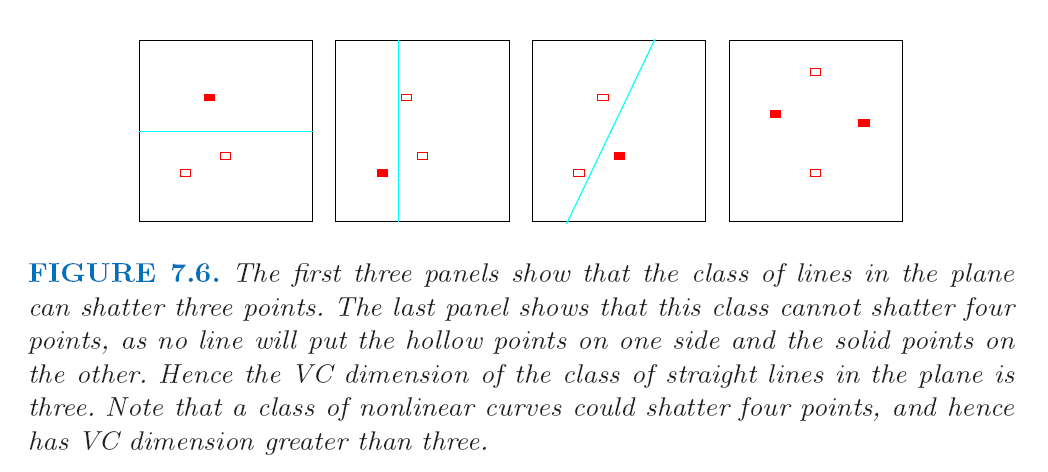
VC维是一种extra-sample的评价指标，提供了一种general的评价模型复杂度的方法。一个模型的VC维，等于这个模型最多可以打散的点的个数，『打散』的意思是，对任意一种正例-负例组合，这个模型都能正确分类。

书上Figure 7.6，第四张图的情况，没有任何一条直线能把两个实心的点分到一边，两个空心的点分到另一边。\(I(\alpha_0 + \alpha_1 x)\)这个模型至多只能打散三个点，因此它的VC维等于\(3\).

可以证明\(I(\sin\alpha \cdot x)\)虽然只有一个可变参数，但是它的VC维是无穷大。这样的模型是不可证伪的，也就是说它可以解释任意给定训练数据。这是没有意义的。

VC维有一些相关的界，这些东西就比较难了，可以去啃Vapnik的大部头。

VC维通常难以估计，常常使用一些upper bound来近似，但这些bound一般比较loose.