不做说明的话，本文讨论的\(x\)都是一维变量

Kernel: 局部方法

这一章讨论的『Kernel』并不是通常我们常说的用于计算内积的那个『Kernel方法』（虽然两者的确是互相联系的），而是一种局部方法，这种方法的模型是整个数据集，考虑最简单的局部方法KNN：

\[\hat{f}(x) = \operatorname{Ave}(y_i | x_i \in N_k(x))\]

这个方法有一个很大的缺陷：仅考虑临近的点，而导致不够smoothing。解决的方法就是将所有的点都考虑进去，并引入kernel function，表征每个点的权重。例如Nadraya-Watson kernel weighted average：

\[\hat{f}(x_0) = \frac{\sum_{i=1}^N K_\lambda (x_0, x_i)y_i}{\sum_{i=1}^N K_\lambda (x_0, x_i)}\]

其中

\[\begin{equation*} \begin{split} K_\lambda (x_0, x) &= D(|x-x_0|/\lambda) \\ D(t) &= \begin{cases} \frac{3}{4}(1-t^2) \quad \text{if} |t|\le 1 \\ 0 \quad \text{otherwise} \end{cases} \end{split} \end{equation*}\]

这其中的\(\lambda\)控制了邻域的大小（宽度）。有了这样一个平滑的kernel function，我们就可以用之于各种局部方法了。例如，在\(x_0\)处做局部线性回归：

\[\min\limits_{\alpha(x_0), \beta(x_0)} \sum\limits_{i=1}^N K_\lambda(x_0, x_i) [y_i - \alpha(x_0) - \beta(x_0) x_i ]^2\]

得到参数估计\(\hat{\alpha}(x_0)\)和\(\hat{\beta}(x_0)\)后，对\(x_0\)的预测值是\(\hat{f}(x_0) = \hat{\alpha}(x_0) + \hat{\beta}(x_0) x_0\)

还可以local log-likelihood：

\[l(\beta(x_0)) = \sum\limits_{i=1}^N K_\lambda (x_0, x_i) l(y_i, x_i^T \beta (x_0))\]

局部密度估计

KNN是一个分类方法，类似于此，我们也可以设计一个局部的密度估计方法：

\[\hat{f}_X (x_0) = \frac{\# x_i \in N(x_0)}{N\lambda}\]

相应的更smooth的Parzen估计为：

\[\hat{f}_X (x_0) = \frac{1}{N\lambda} \sum\limits_{i=1}^N K_\lambda (x_0, x_i)\]

样条基函数和Kernel

样条函数是一种结点处的局部方法，我们同样可以用kernel给它smooth一下，定义模型：

\[\begin{equation*} \begin{split} f(x) &= \sum\limits_{j=1}^M K_{\lambda_j} (\xi_j, x) \beta_j \\ &= \sum\limits_{j=1}^M D\left( \frac{\|x-\xi_j\|}{\lambda_j} \right) \beta_j \end{split} \end{equation*}\]

估计参数\(\{ \lambda_j, \xi_j, \beta_j \}\)，通常定义\(D\)为高斯密度函数，使用最小二乘估计：

\[\min\limits_{\{ \lambda_j, \xi_j, \beta_j \}_1^M} \sum\limits_{i=1}^N \left( y_i - \beta_0 - \sum\limits_{j=1}^M \beta_j \exp \left\{ - \frac{(x_i - \xi_j)^T (x_i - \xi_j)}{\lambda_j^2} \right\} \right)^2\]

我们得到了RBF神经网络，这是一个非凸问题，使用NN常用的求解算法。

当然，如果我们能够给定\(\{\lambda_j, \xi_j\}\)，那么求解\(\beta_j\)就是个简单的最小二乘问题了。为了减少参数个数，有时候我们也会把所有的\(\lambda_j\)用一个hyper-parameter \(\lambda\)来代替，这时候有可能导致多个高斯分布尾端重合处产生洞(holes)，解决这个问题的简单方法就是对样条基函数重新规则化(renormalized)：

\[h_j(x) = \frac{D(\|x-\xi_j\| / \lambda} {\sum\limits_{k=1}^M D(\|x-\xi_k\| / \lambda}\]

如下图所示：

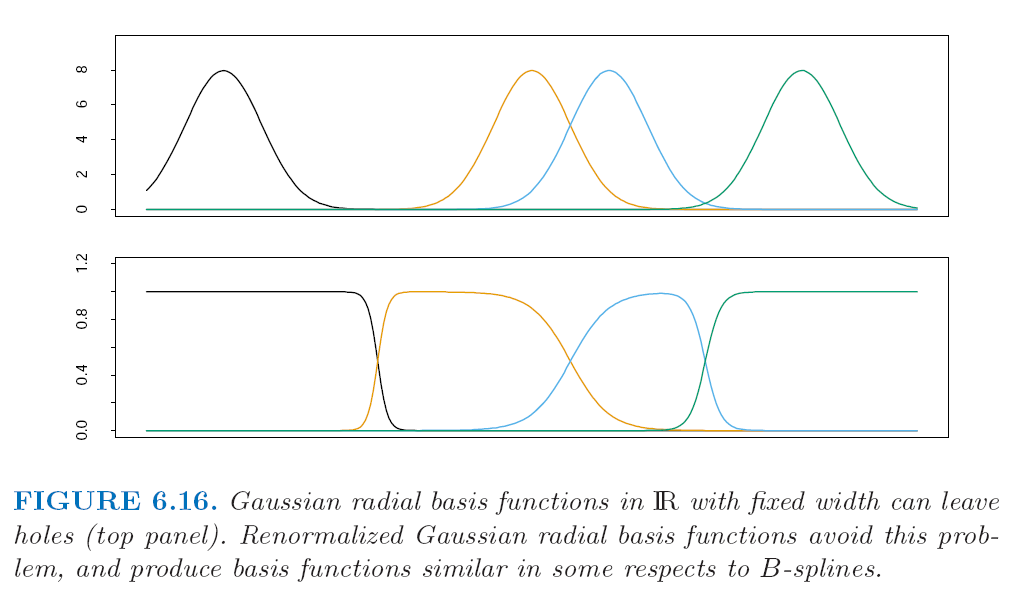
通过样条基函数，计算内积的那个『modern kernel methods』和局部方法(local fitting technology)就联系起来了。